13 Feb 2026
영가설 검정은 많은 분야에서 명제의 참거짓을 판단하는 가장 널리 쓰이는 도구입니다.
흔히 P-value나 신뢰구간으로 대표되는 방식 말입니다.
주로 어떤 모수가 0이라는 시험가설 하에서 관찰된 혹은 그보다 더 극단적인 데이터가 발생할 확률을 계산하여 이 확률이 어떤 기준치보다 작으면 시험 가설을 기각하고 대안 가설을 채택하는 형태입니다.
여기에 두 가지 임의적인 기준이 있습니다.
하나는 데이터를 극단적이라고 판단하는 확률이0.05 같은 숫자로 정해져 있다는 것이고 다른 하나는 기준이 되는 시험가설의 모수를 0으로 가정하는 것입니다.
이렇게 시험가설의 모수가 0일 때 우리는 시험가설을 영가설이라고 부릅니다.
오늘은 두 번째 문제를 중점적으로 왜 통계적 검정에서 메커니즘이 중요한지 다루겠습니다.
왜냐하면 시험가설이 영가설일 이유는 통계학적으로 존재하지 않기 때문입니다.
모수가 0인 가설도, 10인 가설도, 혹은 1억인 가설도 모두 시험가설이 될 수 있습니다.
데이비드 카드와 앨런 크루거는 1994년최저임금에 대한 기념비적인 연구를 발표합니다.
안타깝게도 일찍이 고인이 된 크루거와 달리 카드는 이 업적으로 2021년 노벨경제학상을 수상합니다.
그들은 펜실베니아와 뉴저지가 비슷한 시기에 다른 최저임금 정책을 편 것을 이용해 최저임금이 고용에 미치는 영향을 이중차분법으로 측정하였습니다.
그 결과, 기존의 통념과 다르게 최저임금 인상이 고용에 영향이 없는 것으로 나타났습니다.
이 연구는 최저임금에 대한 경험적 연구를 본격적으로 촉발했을 뿐만 아니라 이중차분법이라는 인과추론 기법을 대중화했다는 점에서도 큰 의의가 있습니다.
하지만 제가 주목할 것은 잘 수행된 미시경제학 연구가 다른 분야와 갖는 중요한 차별점에 대한 것입니다.
겉보기에 이 연구는 여느 다른 논문과 마찬가지로 고용에 미치는 최저임금의 효과가 없는 것을 시험가설로 놓고 회귀분석을 이용하여 최저임금의 고용효과를 측정합니다.
효과가 없는 것을 시험가설로, 효과가 있는 것을 대안 가설로 정하는 것은 얼핏 보기에 다른 연구와 다를 것이 없죠.
그러나 아주 기본적인 경제학을 상기하면 이러한 선택은 경제학적 통념에 완전히 배치되는 것입니다.
경제학적 논의는 대체로 완전경쟁시장에서 출발합니다.
이러한 시장에서는 시장참가자의 효용이 최대화되는 지점에서 평형점이 발생한다는 것을 수학적으로 증명할 수 있습니다.
그래서 대학 교과서에서 가장 먼저 배우는 내용이기도 하고,
동시에 최저임금이나 관세와 같은 외부적인 작용을 반대하는 논거로 널리 쓰입니다.
이러한 시장이 가장 수학적으로 단순하고 직관적이라는 사실은 완전경쟁시장이 경제학에서의 영가설에 해당함을 알려줍니다.
즉, 어떤 미시경제학적 모형이든 그 쓸모를 증명하기 위해서는 완전경쟁시장보다 데이터를 월등히 잘 설명할 수 있어야 합니다.
이 관점에서 보면 카드와 크루거의 영가설 설정은 너무나도 이상합니다.
왜냐하면 완전경쟁시장에서는 최저임금이 평형점에 견주었을 때 고용을 줄이기 때문입니다.
이 상황에서 완전경쟁시장이라는 영가설을 고려하면 회귀분석은 최저임금의 효과가 0인 것을 기각하는 것이 아니라 음의 값을 갖는 것을 기각해야하죠.
반면, 최저임금의 고용효과가 0이기 위해서 우리는 완전경쟁시장이 아닌 다른 시장 메커니즘을 필요로 합니다.
그것이 바로 독점적경쟁시장 (Monopolistic competition) 입니다.
독점적 경쟁시장에서는 동일하지 않은 시장 지배력 (Market power)으로 인해서 최저임금 같은 규제가 오히려 시장의 비효율성을 줄일 수 있습니다.
그 결과, 최저임금이 완전경쟁시장과 다르게 고용에 효과를 미치지 않거나 심지어는 고용을 증가시키는 결과를 가져올 수도 있습니다.
따라서 이론적인 관점에서 보면 완전경쟁시장에서 도출되는 음의 효과가 영가설이 되어야 하고 독점적경쟁시장에서 도출되는 0의 효과가 시험가설이 되어야 합니다.
그런데 여러분은 효과가 0인 것을 기각하는 것이 아닌 효과가 0이 아닌것을 기각하는 연구를 보신 적이 있나요?
카드와 크루거의 연구가 영가설을 기각하지 못했음에도 불구하고 오히려 더 주목을 받은 것은 통계학적으로 유의하지 않은 결과 (영가설을 기각하지 못하였음)에도 불구하고 경제학적으로 기존 이론에 배치되는 결과를 얻었기 때문입니다.
이는 현상의 원리와 메커니즘이 견고한 미시경제학이라는 분야에서 통계적 검정이 진리판단에 미치는 부수적인 역할을 보여줍니다.
현상과 메커니즘에 대한 이해가 없기 때문에 통계적 유의성이라는 외부적인 기준에 의존할 수 밖에 없는 다른 분야와의 큰 차이가 여기 있습니다.
통계학은 통계학일 뿐이며 무엇이 진리인지 판단하는데 보조적인 역할을 할 뿐, 각 분야의 참거짓 여부는 궁극적으로 그 분야의 이론과 메커니즘에 근거한 것이어야 합니다.
그러나 이러한 메커니즘이 부재한 많은 분야의 현실 때문에 통계학적 유의성은 마치 성경 말씀처럼 이해되어 남용되고 있습니다.
제가 병원에 있을 때 논문을 쓰다가 막힌 사람들이 통계고수를 찾는 것을 많이 보았습니다.
다들 그 고수는 뭔가 답을 알고 있을 거라고, 좀 더 적나라하게는 같은 데이터로 통계학적으로 유의한 결과를 낼 방법을 알 거라고 기대하는 것이죠.
하지만 그 전에 통계학적으로 유의한 결과와 그렇지 않은 결과 중 무엇이 더 의학적으로 흥미로운 것인지 스스로 답하는 것이 더 중요하다는 점을 강조하고 싶습니다.
03 Jun 2023
•
Bioinformatics
In the last post, I explained how to add RSIDs to GWAS summary statistics.
Although the final RSID assignment step was fast enough for processing large data, the overall process was quite cumbersome for several reasons.
Most of all, it first extracted the chr:pos to a separate file and then assigned the RSIDs.
Therefore, the user had to combine the original sumstats file with the chr:pos-RSID file manually after obtaining the RSIDs for the variants in chr:pos.
More …
20 Feb 2023
•
Bioinformatics
GWAS summary statistics are frequently shared these days.
They have many usages, for example, an input for LDSC.
However, they are sometimes not formatted properly including the absence of RSID.
When RSID is absent, Chromosome:Position coordinates are there instead.
In theory, it should be possible to map this value to RSID but it’s a demanding task when you have several millions of variants to be queried.
More …
17 Dec 2022
•
Population genetics
Say there are two allels $A_1$ and $A_2$.
There corresponding frequencies are $p$ and $q$.
Let $F$ be the probability that two randomly selected alleles are identity-by-descent (IBD).
More …
03 Jun 2022
이 포스트는 제 연구를 소개하는 글입니다.
이 포스트를 시작으로 진화생물학 및 통계유전학이 사회와 어떤 관계를 맺고 있는지 소개하는 글을 몇 편 쓰려고 합니다.
대중적으로 유명한 진화심리학 등이 과학적 발견의 사회적 의의에 초점을 맞췄다면 저는 반대로 사회적 구조가 유전학 연구에 어떤 영향을 미치는지 다루려고 합니다.
저는 서울대학교 의과대학을 다녔습니다.
서울대학교 의과대학에는 크게 3개의 수련 병원이 있습니다.
연건동에 위치한 서울대학교병원 (소위 본원이라고 불립니다), 분당서울대학교병원 그리고 동작구에 위치한 시립보라매병원입니다.
세 병원은 각각 성격이 다릅니다.
본원이 상급종합병원으로서 암이나 희귀질환 같은 난치성 질환 치료와 연구에 집중한다면 보라매병원은 시립병원으로서 취약계층 진료에 그 목적을 두고 있습니다.
이런 차이는 학생으로 실습기간 동안 충분히 느낄 수 있었습니다.
점심시간이 넉넉한 날이면 현관 근처에서 커피를 마시며 멍때리곤 했는데 과장 조금 보태면 10분에 한 번씩 양복을 입은 기사님이 운전하는 S클래스에서 하차하는 어르신을 봅니다.
온 동네 고급차량은 병원에서 다 본 것 같습니다.
한편, 보라매병원은 완전히 다른 세상입니다.
건강보험료를 지급하지 못하여 공공부조의 일종인 의료급여를 받는 환자가 굉장히 많습니다.
외래에서 뵙는 환자 중에 병이 상당히 진행된 상태에서 내원하는 비수도권 환자도 적지 않게 보입니다.
동시에 요즘은 빅데이터와 인공지능이 각광을 받는 시대입니다.
이런 흐름에 발맞춰 학교와 병원에서도 십수년 간 축적된 환자 데이터를 바탕으로 새로운 지식을 창출하려는 연구를 활발하게 하고 있습니다.
그런데 저는 그런 생각이 들었습니다.
50억 정도 하는 압구정 현대 아파트에 사는 어르신과 경남 양산 시골에 사는 어르신이 서울대병원에 내원할 기회가 동등하지 않은데 이런 편향된 환자의 모임에서 생산된 데이터로 좋은 연구를 할 수 있을까?
인과추론 (Causal inference)는 관찰된 상관관계에서 인과성을 창출하는 방법을 연구하는 분야로 제 의문 역시 인과추론에서 오랫동안 연구된 문제입니다.
이처럼 대표성 없는 자료에서 인과성에서 비롯되지 않는 무의미한 상관관계가 생기는 현상을 선택편향 (selection bias)라고 부릅니다.
선택편향은 우리 생활 곳곳에 퍼져있습니다.
흔히, 많은 기혼 여성이 만났던 사람 중에 현재 배우자가 성격은 좋지만 외모는 제일 못났다고 한탄하곤 합니다.
외모와 인품의 반비례 관계는 어떤 인과성에 의한 것일까요?
선택편향에 대한 이론은 여기에 대한 확고한 답을 줍니다.
외모와 인품 모두 교제의 가능성을 높이기 때문에 (교제가 외모와 인품의 결과이기 때문에) 교제했던 사람만 모아서 보면 둘이 반비례하는 것처럼 보이는 것입니다.
교제가 외모와 인품 모두와 완전히 독립적으로 일어났다면 이런 상관관계는 생기지 않았을 것입니다.
위 같은 이유로 서울대병원의 빅데이터는 여러 요인의 결과로 서울대병원에 내원할 수 있었던 환자만 분석 대상으로 삼기 때문에 앞선 예시와 같은 문제를 겪을 수 밖에 없습니다.
이런 의료 빅데이터의 한 종류로 대규모 유전체 연구가 있습니다.
저는 유전학을 공부하고 이런 자료를 분석하고 있습니다.
그런데 유전체 연구도 연구에 자발적으로 참여하는 사람만 포함하고 있으므로 선택편향으로부터 자유로울 수 없습니다.
그렇다면 그 선택편향의 크기는 얼마고 어떤 요인의 영향을 받는지 밝힐 필요가 있고 제 연구는 정확히 이 문제를 다룹니다.
2021년 네이쳐 유전학 (Nature Genetics)에 출판된 연구는 생물학적 성별과 상염색체 유전 변이 사이의 상관관계를 분석했습니다.
생물학적 성별은 성염색체가 결정하고 상염색체와 무관하므로 아무런 상관관계가 나타나지 않을 것으로 기대할 수 있으나 결과는 충격적이게도 그렇지 않았습니다.
놀랍게도 수백 개의 상염색체 변이가 성별과 상관관계가 있는 것으로 드러났습니다.
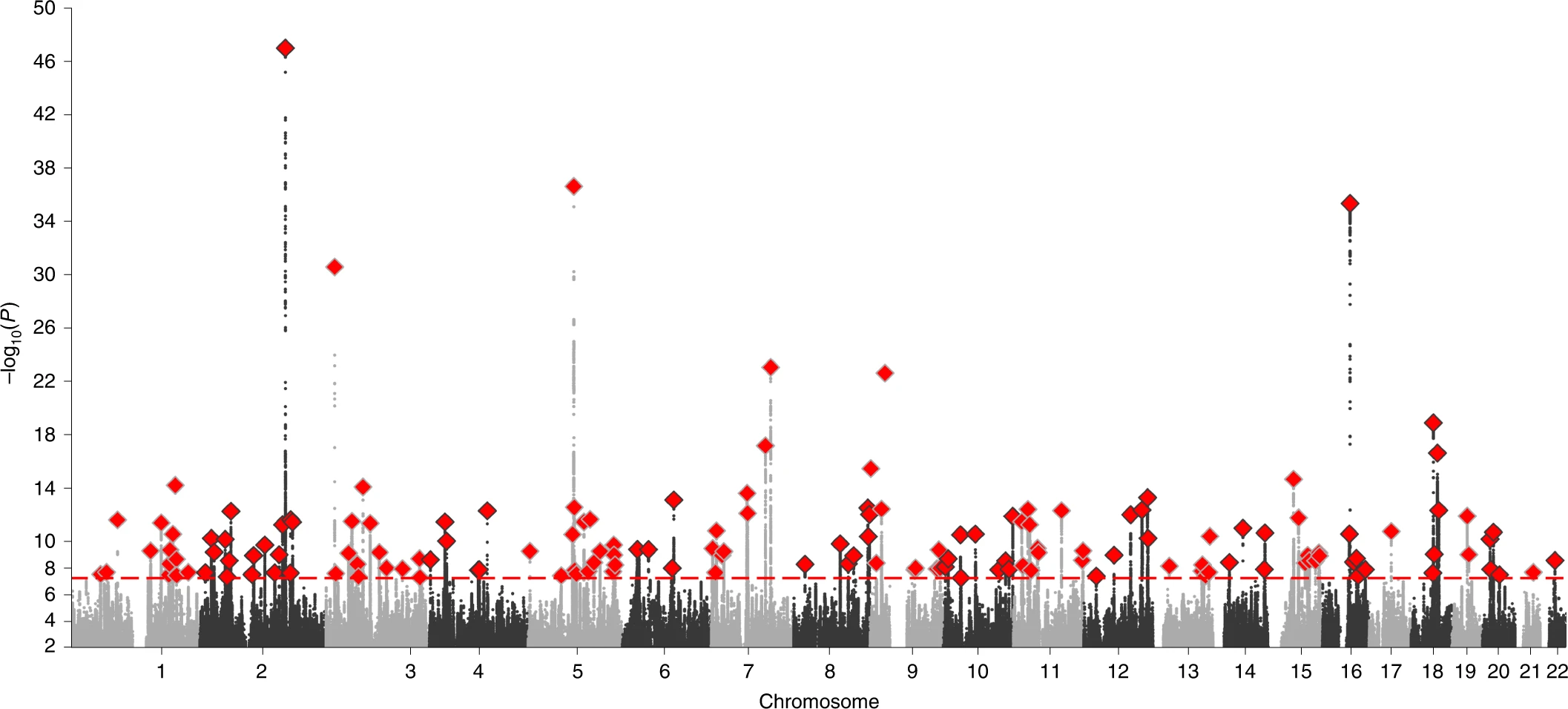
이 연구는 선택편향를 이러한 상관관계의 원인으로 지목했으나 정확히 그 수학적인 기전을 밝히진 못했습니다.
제 연구는 그들이 밝히지 못한 수학적인 기전과 일반적인 이론을 제안하는 것입니다.
왜 이런 연구를 했는지 생각해보면 의과대학에서의 경험이 결정적이었습니다.
저는 대학에 오기까지 20년을 부산에서 살았는데 부산은 제2 도시로서의 위상에도 불구하고 전라권이나 경북권에 비해 의료 환경이 매우 낙후됐습니다.
때문에 서울에서 경험한 의료환경은 그 자체로 놀라운 경험이었고 그 안에서도 본원과 보라매 병원의 차이와 같은 불평등의 결과가 항상 마음 한 켠에 있었습니다.
그런 와중에 네이쳐에 출판된 연구를 접하면서 제 문제의식을 구체화할 수 있는 기회라고 생각하여 금번의 연구를 시작할 수 있었습니다.
비록 논문 본문에 적지 않았지만 제 연구는 몇 가지 중요한 점을 시사하고 있습니다.
하나, 대규모 유전체 연구에서 선택편향을 제거하기 위해서는 각 피연구자가 연구에 참여할 확률을 알아야 합니다.
그리고 그 확률을 알기 위해서는 어떤 경위로 그 사람이 연구에 참여하게 되는지 반드시 이해할 필요가 있습니다.
둘, 이런 사실을 한국의 맥락으로 가져오면 한국은 지역 간 의료불평등과 계층에 따른 의료접근성의 차이가 대단히 큰 나라입니다.
그런 나라에서 아무리 많은 데이터를 바탕으로 연구를 한다고 한들 선택편향으로부터 자유로울 수 없습니다.
때문에 엄밀한 연구를 위해서라도 건강불평등의 원인과 해결책을 고민할 수 밖에 없는 것입니다.
마지막으로, 사회적으로 의료접근성이 균등한 곳일수록 최첨단의 연구가 더 쉽고 간편하다는 것입니다.
그런 사회에서는 의료접근성으로 인한 선택편향이 없을테니까요.
저는 집단유전학과 인과추론의 교집합에 위치한 사람입니다.
그 자체로 의료접근성이나 불평등을 연구하진 않는다는 뜻입니다.
그러나 제가 다루는 자료와 데이터는 사회에서 만들어지고 바로 그렇기 때문에 의료접근성과 불평등을 무시할 수가 없습니다.
금번의 연구는 그 점을 수학적인 관점에서 간접적으로 보여주고 있습니다.